Pular para o conteúdo principal

Teoria dos conjuntos (matemática) - resumo

Teoria dos conjuntos numéricos
Resumo
Lara Araújo
9º ano

Bem, pra começar a falar sobre teoria dos conjuntos, que é um assunto básico da matemática devemos entender o que é um conjunto.
Como "conjunto" compreende-se um grupo de pessoas, objetos, números etc. 

Os conjuntos, nesse assunto, são:
Números naturais (N);
Números inteiros (Z);
Números racionais (Q);
Números irracionais (IR);
Números reais (R).

Um por um, então:

Os números naturais são aqueles que usamos no fundamental, os mais conhecidos e utilizados. Eles começam do 0, ou seja, não são negativos e também não são compostos de dízimas (as dízimas se encaixam num outro conjunto).
Exemplos de números naturais:  0, 1, 2, 3, 4...

 Esse é o símbolo do conjunto dos números naturais.







Os números inteiros são o conjunto que inclui os números naturais, já falados, e também os números negativos, ou seja, abaixo de 0. Sendo assim, o conjunto dos números inteiros inclui o conjunto dos números naturais.
Exemplos de números inteiros: ... -3, -2, -1, 0 , 1, 2, 3...






Esse é o símbolo do conjunto dos números inteiros.






Os números racionais são do conjunto que inclui os dois conjuntos já falados, mas, além dos números naturais e dos números inteiros, ele também contém as frações e as dízimas periódicas (números decimais com repetição de um número, lembra?) ou dízimas exatas. 
Exemplos de números racionais: 1, 2, 3 (naturais) ou -1, -2, -3 (negativos);  1/2 ou 3/7 (frações); 0,7777... ou 9,878787... (dízimas periódicas) e 0,06 ou 0,89 (dízimas exatas).

Números RacionaisNúmeros Racionais





Esse é o símbolo do conjunto dos números racionais.
O conjunto dos números racionais tem algumas classificações como números racionais não-positivos, números racionais não-nulos, números racionais não-negativos, números racionais positivos e números racionais negativos; os nomes de cada um já falam por si só, né?



Os números irracionais (IR) não incluem nenhum outro conjunto, pois incluem apenas as dízimas não períodicas e infinitas.
Exemplos de números irracionais: 
1,7320508... 
√7 = 2,645751...

 Os números reais (R) são o conjunto de todos os números que podem ser localizados numa reta numérica, todos os conjuntos. Ou seja, junção dos naturais, inteiros, racionais, irracionais em um só grupo. 
Exemplos de números reais: 
1,7320508... 
 0,89
 ... -3, -2, -1, 0 , 1, 2, 3...
1/2
9,878787


Aqui vai a famosa imagem que resume bem isso tudo, espero que tenha ajudado :)



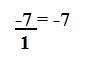
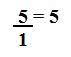
Comentários

Postar um comentário

Postagens mais visitadas deste blog

Civilização asteca: religião, arquitetura, arte, agricultura, etc.

Povos astecas - resumo.  Lara Araújo 9º ano Quando se fala em “astecas”, refere-se ao povo destinado à guerra, que habitaram a atual região do México, entre os séculos XIV e XVI. A sociedade asteca era fortemente hierarquizada, sob os comandos de um imperador, chefe do exército. A maior parte da população, como é de se esperar, tinha como componentes, a maioria, camponeses, trabalhadores, artesãos.             Se hoje temos grandes e desenvolvidas técnicas agrícolas, isso se dá graças a esse povo, que trouxe avanços úteis na área da agricultura, como por exemplo, obras de drenagem e ilhas de cultivo onde eram plantados tomates, pimenta, milho, entre outros produtos. As sementes do cacau que plantavam eram usadas como moeda para a população.             Não só na agricultura como também no artesanato, esse povo era demasiado desenvolvido para o tempo em que ex...
Postar um comentário
Leia mais

Origem da equação de 2º grau

A origem da equação de segundo grau - resumo  Lara Araújo (9º Ano) A equação de segundo grau que conhecemos atualmente, é, na verdade, resultado de diversas transformações e de vários estudos.  O começo dessa história, vem desde aproximadamente 1950 a.C., quando surgem papiros como o Papiro de Berlim, escrito pelos egípcios. Esse povo compôs grandes avanços iniciais para a resolução da equação de 2º grau. Encontra-se, por exemplo, no Papíro de Kahun, o método da falsa posição na resolução de uma equação, hoje escrita x² + y² =K, sendo K um número positivo; esse método foi desenvolvido pelos egípcios para a resolução da equação de 1º grau.  Já na Mesopotâmia, o primeiro registro com resolução de problemas que envolviam a equação de 2º grau, data de 1700 a.C. Esse registro foi feito numa tábua de argila através de palavras. Foi na Grécia, finalmente, que se encontra soluções das equações de 2º grau. Essa civilização desenvolveu um tratamento geométrico de diverso...
Postar um comentário
Leia mais